Um beijo , um momento especial , o luar.
Depois sinto que tudo é oco.
Observando o que vejo
O que vejo e sinto
para transformar em palavras
e preencher o vazio.
Misturando a argila
Um vaso, eu faço
Recheado de saudade
Mas, sei que é o oco do vaso
Que lhe dá utilidade
Assim, também as paredes
Que dão contorno à morada
São construídas com massa
Mas, é no espaço vazio
Que encontro o essencial
Concluo então pessoal
Que as coisas físicas
Parecem o principal
Mas é no metafísico
Que está o valor real.
by AnnGeliKa
O vazio,
cheio de vazio,
que preenche o vazio,
novo vazio que se forma,
dessa forma ama-se pra sempre,
numa espiral
do coração fractal.
By Simão
O QUE É FRACTAL?
Fractais (do latim fractus, fração, quebrado) são figuras da geometria não-Euclidiana.
A geometria fractal é o ramo da matemática que estuda as propriedades e comportamento dos fractais. Descreve muitas situações que não podem ser explicadas facilmente pela geometria clássica, e foram aplicadas em ciência, tecnologia e arte gerada por computador. As raízes conceituais dos fractais remontam a tentativas de medir o tamanho de objetos para os quais as definições tradicionais baseadas na geometria euclidiana falham.
Um fractal (anteriormente conhecido como curva monstro) é um objeto geométrico que pode ser dividido em partes, cada uma das quais semelhante ao objeto original. Diz-se que os fractais têm infinitos detalhes, são geralmente auto-similares e independem de escala. Em muitos casos um fractal pode ser gerado por um padrão repetido, tipicamente um processo recorrente ou iterativo.
O termo foi cunhado em 1975 por Benoît Mandelbrot, matemático francês nascido na Polónia, que descobriu a geometria fractal na década de 70 do século XX, a partir do adjetivo latino fractus, do verbo frangere, que significa quebrar.
Vários tipos de fractais foram originalmente estudados como objetos matemáticos.
Exemplos

Árvores e samambaias (ou fetos) são fractais naturais que podem ser modelados em computadores que usam algoritmos recursivos. Esta propriedade de repitividade está clara nestes exemplos, pois num ramo de uma árvore ou na folhagem de uma samambaia pode ser observada uma réplica em miniatura do todo. Não idêntico, porém semelhante na estrutura.
Uma classe relativamente simples de exemplos é o Cantor que observado num intervalo (digamos 1:1) e então noutro (1:10) mais curto (ou aberto), visto numa escala de 0, 1, é uma figura que pode (ou não pode) ser “ego-semelhante” em determinada amplificação, e pode (ou não pode) ter uma dimensão d ou 0 < d <>
Um exemplo simples seria excluir o dígito 7 de expansão decimal, ego-semelhante sob dobra-10 (ou amplificação), e também ter uma dimensão tronco 9/log 10 (este valor é o mesmo, não importa que base logarítmica é escolhida), mostrando assim a conexão dos dois conceitos.
Os Fractais são geralmente corrugados na sua forma (tanto em cálculos quanto nas imagens resultantes destes), Portanto, não são objetos definíveis pela geometria tradicional. Isso quer dizer que os fractais tendem a ter detalhes significantes, visíveis sob qualquer ponto de vista (ou seja, suas variações visuais são perfeitamente mensuráveis); quando houver uma ego-semelhança, isto pode ocorrer porque ao se observar sob “zoom” figuras semelhantes observaremos a recursividade, ou repitividade destas.

Por exemplo, numa forma euclidiana normal (como um círculo) esta parece mais aplainada e alisada quando é amplificada. Numa ampliação infinita seria impossível se diferenciar entre o círculo e uma linha reta. No caso dos fractais, isto não acontece (embora, quanto mais amplificarmos, mais nos aproximaremos da linha reta também - isto ocorre devida perda de dados em múltiplas amplificações- ou seja, os desvios acontecem devida imprecisão das inserções seqüenciais dos dados).
A idéia convencional de curvatura representada pela reciprocidade radial (em radianos) num círculo por aproximação, não pode ser usualmente aplicada em escalas muito grandes (neste caso, o “raio” de curvatura ficará fora de escala, daí a “aparência” de uma linha reta).
Ao contrário, com fractais, ao se aumentar a amplificação, se revelarão mais e mais detalhes. Estes dependerão do grau de precisão e da quantidade de casas decimais dos dados inseridos. As distorções tendendo para a linha reta, ocorrem justamente pelo fato de haver “falta de memória” nas máquinas que executam o cálculo. Portanto, um fractal jamais alcançará uma linha reta, salvo quando a fórmula que o constitui assim o permita.
Alguns exemplos comuns de fractais:
- Conjunto de Mandelbrot
- Fractal de Lyapunov
- Conjunto de Precentor
- Tapete de Sierpinski
- Triângulo de Sierpinski
- Menger sponge
- Curva de dragão
- Curva de Peano
- Curva de Koch
Os Fractais podem ser determinísticos ou estocásticos (Ver George G. Stokes).
No caso da Teoria do Caos, podemos associa-la totalmente aos fractais, também no conhecido “Mandelbrot set” Conjunto de Mandelbrot podemos observar discos inteiros, cuja dimensão é 2. Isto não é de surpreender, porém o que é verdadeiramente surpreendente é que o limite do conjunto Mandelbrot também tem uma dimensão de Hausdorff de 2.

Aproximações de fractais (Fractais naturais) são encontrados freqüentemente na natureza. Estes objetos exibem uma estrutura complexa próxima aos objetos matemáticos, porém finitas se as observarmos em maiores escalas.
Os fractais naturais estão à nossa volta, basta observarmos as nuvens, as montanhas, os rios e seus afluentes, os sistemas de vasos sanguíneos, os feixes nervosos, etc. Com maiores ou menores graus, estas figuras estão classificadas em diversas magnitudes.
Apesar de existirem por toda a natureza, e de serem onipresentes, estes objetos somente foram realmente estudados a fundo no século XX.
Harrison [1] estendeu o cálculo Newtoniano para o domínio fractal, também inseriu os teoremas Gauss da divergência, o Teorema de Green, e o Teorema de Stoke.
Os Fractais são normalmente gerados através de computadores com softwares específicos. Através de seu estudo podemos descrever muitos objetos extremamente irregulares do mundo real. Como exemplo de softwares temos o Xaos -http://xaos.sourceforge.net/index.php.
Os meteorologistas utilizam o cálculo fractal para verificar as turbulências da atmosfera incluindo dados como nuvens, montanhas, a própria turbulência, os litorais, e árvores. As técnicas fractais também estão sendo empregadas para a compactação de imagens através da compressão fractal, além das mais diversas disciplinas científicas que utilizam o processo.
[editar] Montanhas fractais
A superfície de uma montanha pode ser modelada num computador usando uma fractal: Começamos com um triângulo no espaço 3D. Acham-se os pontos centrais das 3 linhas que formam o triângulo e criam-se 4 novos triângulos a partir desse triângulo. Deslocam-se depois aleatoriamente esses pontos centrais para cima ou para baixo dentro de uma gama de valores estabelecido. Vai-se repetindo o mesmo procedimento mas fazendo os deslocamentos dos pontos centrais dentro de uma gama de valores que em cada iteração é igual a metade da anterior.
[editar] Computação de um feto (ou samambaia)
Um feto fractal pode ser gerado usando um sistema de funções iteradas começando com um ponto na origem  e determinando iterativamente novos pontos a partir do resultado da aplicação aleatória de uma de 4 diferentes transformações de coordenadas:
e determinando iterativamente novos pontos a partir do resultado da aplicação aleatória de uma de 4 diferentes transformações de coordenadas:

Esta transformação, que é realizada apenas 1% das vezes, mapeia qualquer ponto para um ponto no segmento de recta mostrado a verde na figura.

Esta transformação, que é realizada apenas 7% das vezes, mapeia qualquer ponto dentro do rectângulo preto para um ponto dentro do rectângulo vermelho na figura.

Esta transformação, que é realizada apenas 7% das vezes, mapeia qualquer ponto dentro do rectângulo preto para um ponto dentro do rectângulo azul escuro na figura.
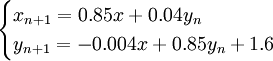
Esta transformação, que é realizada 85% das vezes, mapeia qualquer ponto dentro do rectângulo preto para um ponto dentro do rectângulo azul claro na figura.
A primeira transformações de coordenadas desenha o caule. A segunda, desenha a primeira folha da esquerda do feto. A terceira, desenha a primeira folha da direita do feto. E a quarta gera cópias sucessivas e garante que o todo é uma réplica maior de cada folha.
[editar] Caos
A Teoria do Caos é conhecida há vários séculos e representada em sabedoria popular:
Por vontade de um prego, a ferradura foi perdida; Por vontade de uma ferradura, o cavalo foi perdido; Por vontade de um cavalo, o cavaleiro foi perdido; Por vontade de um cavaleiro, a batalha foi perdida; Por vontade de uma batalha, o reino foi perdido.
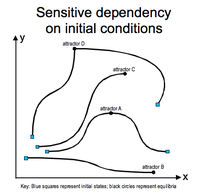
O resultado de uma condição inicial sujeita a pequenas variações é completamente diferente do original. Nesse folclore, é o mesmo que dizer que por vontade de um prego, o reino foi perdido.
Apesar dos efeitos da Teoria do Caos estarem tão presentes no nosso dia, como na meteorologia, na irregularidade da pulsação cardíaca, no gotejar de uma torneira, no relampejar, nas montanhas, nas árvores, no crescimento de uma população, no partir de um copo no chão e por aí fora, só há alguns anos começou a ser estudada, talvez porque antes, sem recurso a computadores, os cálculos necessários, que são bastante repetitivos, fossem aborrecidos demais.
Curiosamente, a primeira verdadeira experiência sobre o caos foi feita por um meteorologista, Edward Lorenz. Nas suas previsões sobre o tempo, geradas através de um programa de computador que tinha desenvolvido, constatou que, mesmo introduzindo grande parte da mesma seqüência no padrão original, o resultado final era diferente. Isso aconteceu um dia, quando, ao tentar verificar uma mesma seqüência, começou pelo meio para poupar tempo. Ele introduziu apenas os três primeiros números da seqüência de seis. Quando resolvida, verificou que o padrão obtido era completamente diferente do alcançado na seqüência anterior. Desta forma, Lorenz demonstrou que mesmo tendo uma seqüência muito próxima da original, seria muita sorte atingir o mesmo resultado. Esse efeito ficou conhecido como “efeito borboleta”. A diferença entre os pontos iniciais de duas curvas distintas é tão pequena que é comparada ao bater das asas de uma borboleta. E o simples bater das asas de uma borboleta, hoje, produz uma pequena alteração na atmosfera que pode, num determinado espaço de tempo, produzir um efeito diferente do que iria acontecer. Diz-se que o bater das asas de uma borboleta em Portugal pode provocar um tornado na China, ou fazer com que um tornado na Flórida não aconteça.[1]










Nenhum comentário:
Postar um comentário